7. 트리(Tree)
7.1 트리의 개념
트리는 앞서 봤던 자료구조와는 달리 비선형 자료구조이다.
데이터를 어떻게 삽입하고 삭제, 검색할 것인지에 대한 관심보다는 데이터를 어떻게 표현하는지에 더 중점을 둔 자료구조이다.
트리는 노드와 노드들을 연결하는 간선으로 이루어져 있다.
7.2 트리 용어
- 루트 노드(root node) : 부모가 없는 노드. 트리는 하나의 루트 노드만을 가진다.
- 단말 노드(leaf node) : 자식이 없는 노드이다.
- 간선(edge) : 노드를 연결하는 선
- 형제(sibling) : 같은 부모를 가지는 노드.
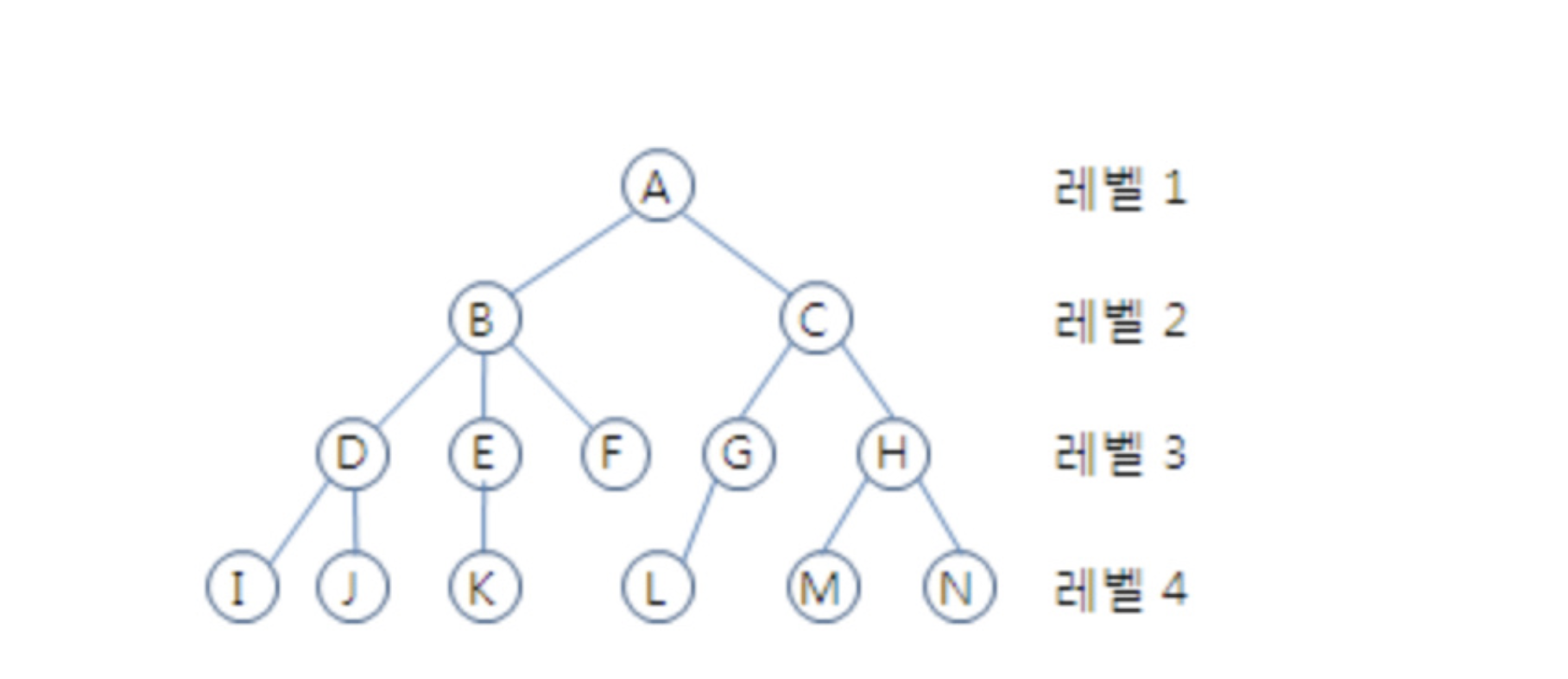
노드의 크기 : 자신을 포함한 모든 자손 노드의 개수 <-> 차수
노드의 깊이 : 루트에서 노드까지 간선의 개수 (B : 1, K : 3)
노드의 레벨 : 루트에서부터 지하로 층수 (A : 1, M : 4)
노드의 차수 : 자식 노드의 개수 (가지의 수) (B : 3)
트리의 차수 : 모든 노드의 차수 중 제일 큰 값 (3)
트리의 높이 : 최고 깊이 (3)
7.3 이진 트리(Binary Tree)
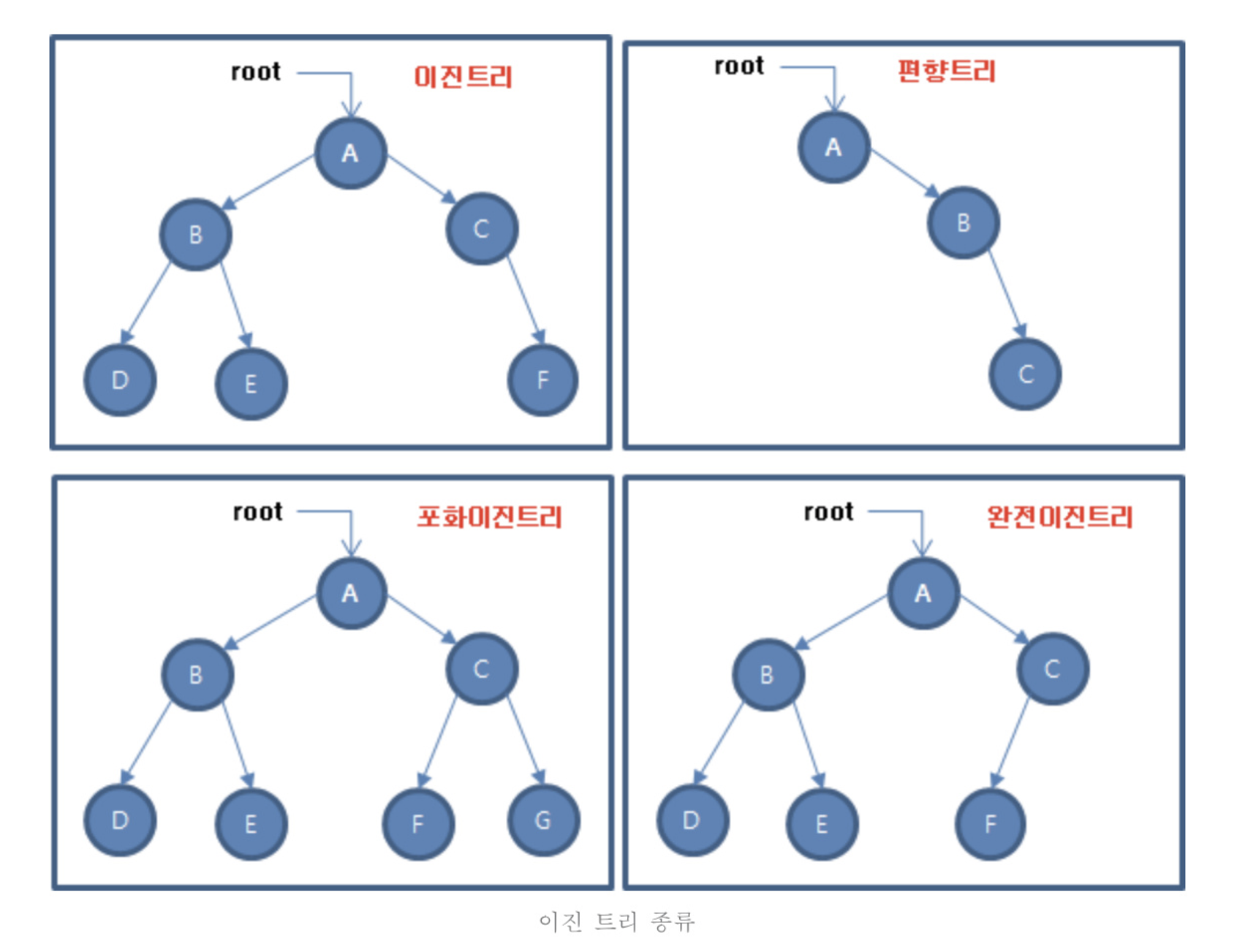
- 포화 이진 트리(full binary tree) : 모든 레벨에서 노드들이 모두 채워져 있는 트리
- 완전 이진트리(complete binary tree)
- 마지막 레벨을 제외하고 노드가 모두 채워져 있는 트리
- 마지막 레벨도 오른쪽으로 연속된 몇개의 노드만 비어있을 수 있음
- 왼쪽부터 차례로 채워나감
7.4 이진 탐색 트리 (Binary Search Tree)
이진 탐색 트리를 정의하면 다음과 같다.
- 어떤 노드의 왼쪽 자식과 오른쪽 자식은 모두 이진 탐색 트리구조를 이룬다.
- 어떤 노드의 왼쪽 자식은 이 노드보다 모두 작고, 오른쪽 자식은 이 노드보다 모두 크다.
이진 탐색 트리는 이름에서 알 수 있듯이, 삽입이나 삭제보다는 탐색에 주 목적을 둔 자료구조이다.
BST에서 가장 구현이 복잡한 것은 delete이다.
자식이 없는 노드나 자식이 하나만 있는 노드는 적당히 부모노드와의 관계만 새로 정의해주고 삭제하면 되지만,
자식이 둘 있는 노드는 조금 복잡하다.
자식이 둘 있는 경우, 왼쪽 자식의 서브트리에서 최대값을 찾거나, 오른쪽 자식의 서브트리에서 최소값을 찾아서 삭제할 노드와 바꿔야 한다.
위의 코드의 경우에는 왼쪽 자식의 서브트리에서 최대값을 찾았다.
'자료구조' 카테고리의 다른 글
| [파이썬 | 자료구조] 9. 그래프(Graph) (1) | 2020.09.06 |
|---|---|
| [파이썬 | 자료구조] 8. 힙(Heap) (0) | 2020.09.04 |
| [파이썬 | 자료구조] 6. 해시 테이블(Hash Table) (0) | 2020.09.04 |
| [파이썬 | 자료구조] 5. 연결 리스트(Linked List) (0) | 2020.09.03 |
| [파이썬 | 자료구조] 4. 스택(Stack) (0) | 2020.09.03 |
